Metrics and Analysis of Load Testing : Mean and Standard Deviation

Let’s cut right to the chase and state how it is. Mean and standard deviation aren’t useful as metrics and analysis in load testing. In fact, they can be very deceptive, with multiple analysis bias. If you are not comfortable with Gatling reports analysis, we advise you to start with our other analytics article. As for Cloud users, we also have that covered in an article dedicated to Cloud reports.

We use most of our time to look at metrics while doing load testing. Thus, we need to make sure it is spent as efficiently as we can. With that in mind, which metrics should we use to have a clear view of what is happening at any point in time? Are these actually useful? Metrics – An Analysis of Load Testing is all about digging into common metrics, understanding their common pitfalls, and avoiding missing changes in your application behavior while load testing.

Definitions

Mean

The mean—arithmetic average, describes the central value of a data set. The standard definition is the sum of all parts divided by the number of parts. Hence, for 𝓃 parts :

The arithmetic average, also written 𝑥̄, is a summary of central tendency. It is easy to use, compute and so far, widely used.

Variance

The variance is a bit more involved. It describes how much values are spread around the mean. You can find the variance by subtracting each part of the data set by its arithmetic average, squared, then dividing by the number of parts.

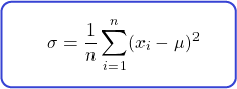
Before we dive into it’s actual sense, let’s go right to the standard deviation.

Standard deviation

The standard deviation is the same as the variance. You express it in the same unit as the mean, whereas you express the variance in squared units. You can use both interchangeably as long are you are rigorous with what units you are using.

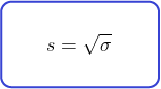
Is it easier to think about the standard deviation as a description of variability rather than its formula. In fact, this is all the mathematics we’ll see for today. Hope you’re okay.

A little bonus: you can differentiate distributions with the same arithmetic average by their standard deviation:

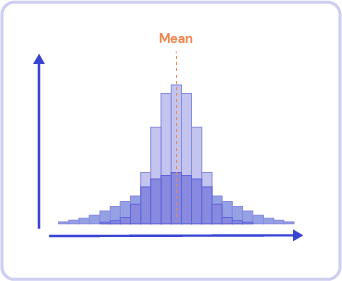
Two distributions with the same average, but different standard deviations

Why does deviation matter in load testing? 

When you use variance and/or standard deviation as metric, you need to make sure which distribution you are dealing with. Knowing how much your data set is spread around the mean doesn’t account for much if you have no idea how the data looks in the first place.
Even worse, how to make sense of the standard deviation if your data is shared between multiple binomial distributions—or, multi modal distributions, like this one:

Multi modal distribution, showing its arithmetic average doesn’t tell much about its shape

Such a data set could be split into multiple sub data sets, then studied individually. Arguably, that would be cumbersome to do, which would defeat our initial purpose of gaining time when analyzing our metrics.

Furthermore, what happens when the mean and standard deviation are the same? Does this mean the data sets are the same? In fact, it is easy to craft distributions with these kind of properties:

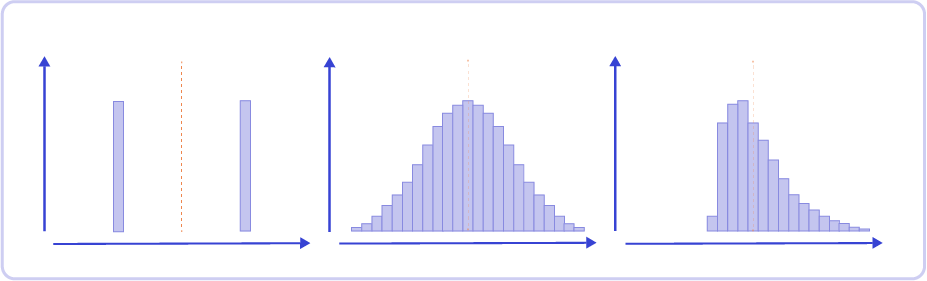
Multiple distributions, sharing the same arithmetic average and standard deviation

Some people went even further as to squash all sorts of shapes with the same average, standard deviation, on both axes, in a single animation. That says a lot about how deviations are as a metric.

https://edubirdie.com/blog/same-stats-different-graphs

As you understand now, variance and standard deviation only make sense on Gaussian distributions, which are rarely encountered in the context of load testing. Most common cases are multi modal distributions, outliers or extreme values, long tails or skewed distributions, and so on.

The arithmetic average is very sensitive to outliers and it won’t tell us much about the shape of the distribution anyway. We will need a more powerful tool to deal with all these cases, which could be stated as extreme if they were not so common!

Then, why are they used?

Mean and standard deviation are metrics that are easy to use and compute. However, they will only be efficient if the distribution is perfectly shaped—i.e., symmetric. That is not the case in the world of load testing, by far.

But then, what to do? What metrics can you use for a good analysis? You can find some answers if you come back to the objectives of a load test. Ultimately, you have to understand what you want to unveil first if you want to choose the good indicators to follow.

Let us know about your project

Used by over 100,000 web applications and e-commerce websites, Gatling solution is put to use in diverse industries including Software, Streaming media, Banking, Insurance, Gaming and Finance.

Related resources

You might also be interested in…